Table Of Content
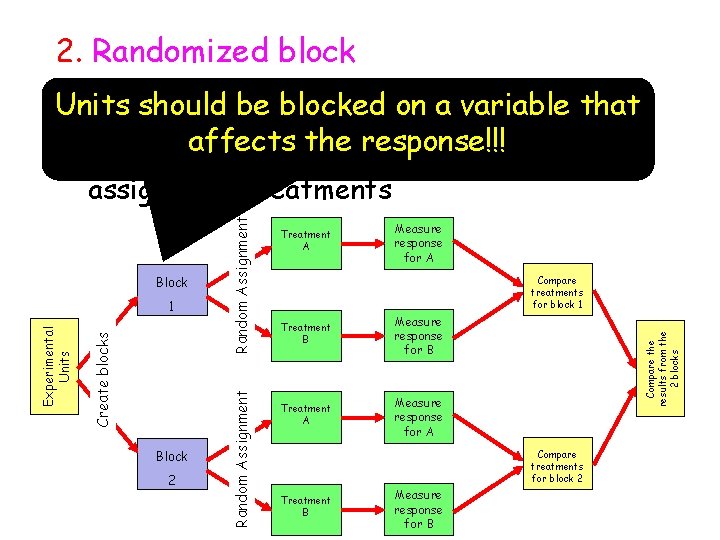
The general linear test is the most powerful test for this type of situation with unbalanced data. Before high-speed computing, data imputation was often done because the ANOVA computations are more readily done using a balanced design. There are times where imputation is still helpful but in the case of a two-way or multiway ANOVA we generally will use the General Linear Model (GLM) and use the full and reduced model approach to do the appropriate test. Here we have four blocks and within each of these blocks is a random assignment of the tips within each block. Another way to think about this is that a complete replicate of the basic experiment is conducted in each block. In this case, a block represents an experimental-wide restriction on randomization.
6 - Crossover Designs
We can see in the table below that the other blocking factor, cow, is also highly significant. For an odd number of treatments, e.g. 3, 5, 7, etc., it requires two orthogonal Latin squares in order to achieve this level of balance. For even number of treatments, 4, 6, etc., you can accomplish this with a single square. This form of balance is denoted balanced for carryover (or residual) effects.
Partially balanced designs (PBIBDs)
Randomization helps distribute the effects of nuisance variables evenly across treatment groups. Proteomics has many aspects that oughtto be taken into accountwhen designing and planning experiments. The complexity of the samples,the proteome, and the analytical techniques employed make proteomicsexperiments particularly challenging. Especially in larger studies,the labor intensive sample preparation often means that the experimenthas to be split into multiple batches. It is therefore important todesign the experiment in such a way that variables and batches arenot confounding.
Difficulty in choosing the number of blocks
For instance, if you had a plot of land the fertility of this land might change in both directions, North -- South and East -- West due to soil or moisture gradients. As we shall see, Latin squares can be used as much as the RCBD in industrial experimentation as well as other experiments. Many such cases are discussed in.[7] However, it can also be observed trivially for the magic squares or magic rectangles which can be viewed as the partially balanced incomplete block designs.
Assign treatments to blocks
State Street 2024 - Planning - DPCED - City of Madison, WI
State Street 2024 - Planning - DPCED.
Posted: Mon, 08 Apr 2024 07:00:00 GMT [source]
The inclusionof a common reference sample is especially importantwhen doing longitudinal/time-series experiments where samples areextracted from patients at multiple time-points. Processingthe samples as they become available can however introduce other confounders,e.g., machine performance or batches of chemicals. The solution isto process the samples at set time-points, and apply the same commonreference sample across the entire experiment. The common referencesample then has to be present in every batch and its placement inthe batch ought to be randomized.

1 - Blocking Scenarios
It is important to have all sequences represented when doing clinical trials with drugs. Here is a plot of the least squares means for Yield with all of the observations included. Where F stands for “Full” and R stands for “Reduced.” The numerator and denominator degrees of freedom for the F statistic is \(df_R - df_F\) and \(df_F\) , respectively.
When the size of the batches is insufficient toachieve this, it is essential to make sure that the utilized experimentaldesign can give answers to the scientific questions asked. Without the blocking variable, ANOVA has two parts of variance, SS intervention and SS error. All variance that can't be explained by the independent variable is considered error. By adding the blocking variable, we partition out some of the error variance and attribute it to the blocking variable. As a results, there will be three parts of the variance in randomized block ANOVA, SS intervention, SS block, and SS error, and together they make up SS total. In doing so, the error variance will be reduced since part of the error variance is now explained by the blocking variable.
Additionally, a substantialnumber of subjects per category is a requirement to still be ableto randomize subjects. If each subject ends up being its own category,randomization will no longer be possible. If different processing steps of the protocol have differentsizeconstraints, i.e., one step requires more batches than another, beingable to combine the smaller batches into larger batches without havingto split the smaller batches is ideal. For example, when one experimentalstep can process 12 samples at once, while another step can process24 samples at once, two batches from the first step can be combinedfor the second processing step. When this is not possible, it makesmost sense to set up the batches according to the smallest constraints,and keep these batches throughout.
What is blocking in experimental design?
We have not randomized these, although you would want to do that, and we do show the third square different from the rest. The row effect is the order of treatment, whether A is done first or second or whether B is done first or second. So, if we have 10 subjects we could label all 10 of the subjects as we have above, or we could label the subjects 1 and 2 nested in a square.
When the numerator (i.e., error) decreases, the calculated F is going to be larger. We will achieve a smaller P obtained value, and are more likely to reject the null hypothesis. In other words, good blocking variables decreases error, which increases statistical power.
This is similar to the situation where we have replicated Latin squares - in this case five reps of 2 × 2 Latin squares, just as was shown previously in Case 2. For most of our examples, GLM will be a useful tool for analyzing and getting the analysis of variance summary table. Even if you are unsure whether your data are orthogonal, one way to check if you simply made a mistake in entering your data is by checking whether the sequential sums of squares agree with the adjusted sums of squares.
Researchers will group participants who are similar on this control variable together into blocks. This control variable is called a blocking variable in the randomized block design. The purpose of the randomized block design is to form groups that are homogeneous on the blocking variable, and thus can be compared with each other based on the independent variable. The single design we looked at so far is the completely randomized design (CRD) where we only have a single factor. In the CRD setting we simply randomly assign the treatments to the available experimental units in our experiment.
This Lego experiment shows our brains prefer adding. Here's why it matters - World Economic Forum
This Lego experiment shows our brains prefer adding. Here's why it matters.
Posted: Wed, 21 Apr 2021 07:00:00 GMT [source]
Since \(\lambda\) is not an integer there does not exist a balanced incomplete block design for this experiment. Seeing as how the block size in this case is fixed, we can achieve a balanced complete block design by adding more replicates so that \(\lambda\) equals at least 1. It needs to be a whole number in order for the design to be balanced. Here we have treatments 1, 2, up to t and the blocks 1, 2, up to b.
Similarly, when all Treatment subjects arein one batch and all Placebo in the other, batchand treatment are confounded and without a batch-independent referenceit is not possible to distinguish the treatment effect from a possiblebatch effect. Thus, it is important to account for control variablesin the experimental design and in the sample organization, and thiscan also be achieved using block randomization. While it is true randomized block design could be more powerful than single-factor between-subjects randomized design, this comes with an important condition. As you have seen from the procedure described above, it shouldn't come as a surprise that it is very difficult to include many blocking variables.
Also, as the number of blocking variables increases, we need to create more blocks. Each block has to have a sufficient group size for statistical analysis, therefore, the sample size can increase rather quickly. The selection of blocking variables should be based on previous literature. When we have a single blocking factor available for our experiment we will try to utilize a randomized complete block design (RCBD). We also consider extensions when more than a single blocking factor exists which takes us to Latin Squares and their generalizations. When we can utilize these ideal designs, which have nice simple structure, the analysis is still very simple, and the designs are quite efficient in terms of power and reducing the error variation.

No comments:
Post a Comment